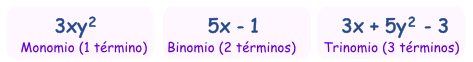¿Para qué sirven los
polinomios?
Bueno, los polinomios están
muy ligados al álgebra. Resolver ecuaciones algebraicas, por ejemplo, es
equivalente a hallar los ceros o raíces de un polinomio. Es por ello que
aprender a factorizar y completar cuadrados, te permitiría no sólo hallar los
valores de x que anulan a un
polinomio, sino también resolver ecuaciones algebraicas.
Cuando enseñan polinomios,
normalmente enseñan que para sumar o restar dos términos éstos deben ser
semejantes; que la multiplicación de polinomios se hace a través de la
propiedad distributiva; que algunas multiplicaciones (o productos) son
notables; que es posible convertir algunos polinomios en productos de dos o más
factores (factorización); que la división de polinomios permite simplificar
expresiones y que todo esto permite manipular fracciones algebraicas. El
objetivo es claro: enseñar a manipular expresiones algebraicas, conocimiento
que es fundamental para cualquier curso de álgebra y cálculo. Quizá es
ésta la utilidad más importante de los polinomios.
Otra utilidad, aunque es más de las funciones en general,
es que los polinomios permiten expresar una serie de operaciones de forma
simbólica. Por ejemplo, si los dulces rojos cuestan 100 Pesos cada uno y
los dulces azules cuestan 50 pesos cada uno, y compro una cantidad "x" de dulces rojos y una
cantidad "y" de
dulces azules, entonces debo pagar 10x
+ 5y (Traducción: multiplico 100 por la cantidad de dulces rojos y le
sumo eso al resultado de multiplicar 50 por la cantidad de dulces azules) Se
escribiría entonces:
P(x,y) = 100x +50y
Si quiero saber cuánto debo pagar si compro 3 chocolates y 4 caramelos, entonces evaluamos el polinomio
(que no es más que sustituir los valores de "x" y "y"):
Dulces rojos = chocolates
Dulces azules = caramelos
P(3,4) = 100 (3) + 50 (4) = 300 + 200
= 500
Entonces 500 es la respuesta.
Es decir, tendría que pagar
500 Pesos en total. Y por supuesto que todo esto se puede hacer sin polinomios,
pero manejar de forma simbólica una serie de operaciones (ya sean funciones
polinómicas o no), permite a las industrias, por ejemplo, hacer análisis sobre
el costo de sus productos, el funcionamiento de sus equipos, la productividad
de sus empleados, etc.
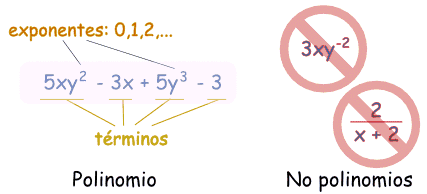
Un polinomio es así:
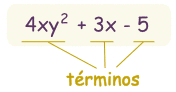 |
un ejemplo de polinomio
este tiene 3 términos |
Están hechos de:
Que se pueden combinar usando:
| + - × |
sumas, restas y multiplicaciones... |
|
 ... ¡pero no divisiones! ... ¡pero no divisiones! 
|
Estas reglas hacen que los polinomios sean simples, ¡así es fácil trabajar con ellos!
¿Son polinomios o no?
Estos
son polinomios:
- 3x
- x - 2
- 3xyz + 3xy2z - 0.1xz - 200y + 0.5
Y estos
no son polinomios
- 2/(x+2) no lo es, porque dividir no está permitido
- 3xy-2 no lo es, porque un exponente es "-2" (los exponentes sólo pueden ser 0,1,2,...)
Pero esto
sí está permitido:
- x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
- también 3x/8 por la misma razón (la constante es 3/8, o 0.375)
2
Entonces hay nombres especiales para los polinomios con 1, 2 o 3 términos:
Monomios, binomios, trinomios
___________________________________________________________________________
___________________________________________________________________________
2DA PARTE
En esta segunda parte veras suma y resta de polinomios, espero te ayude a comprender de mejor manera este tema.
Observa el siguentye LINK
Este video te ayudara a comprenderlo de mejor forma